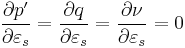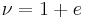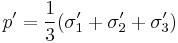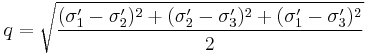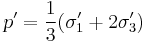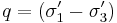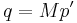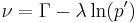Critical state soil mechanics
Critical State Soil Mechanics is the area of Soil Mechanics that encompasses the conceptual models that represent the mechanical behavior of saturated remolded soils based on the Critical State concept.
Contents |
Formulation
The Critical State concept is an idealization of the observed behavior of saturated remoulded clays in triaxial compression tests, and it is assumed to apply to undisturbed soils. It states that soils and other granular materials, if continuously distorted (sheared) until they flow as a frictional fluid, will come into a well-defined critical state. At the onset of the critical state, shear distortions 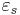 occur without any further changes in mean effective stress
occur without any further changes in mean effective stress 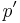 , deviatoric stress
, deviatoric stress 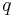 (or yield stress,
(or yield stress, 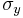 , in uniaxial tension according to the von Mises yielding criterion), or specific volume
, in uniaxial tension according to the von Mises yielding criterion), or specific volume 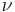 :
:
where,
However, for triaxial conditions  . Thus,
. Thus,
All critical states, for a given soil, form a unique line called the Critical State Line (CSL) defined by the following equations in the space 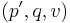 :
:
where 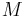 ,
, 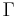 , and
, and 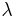 are soil constants. The first equation determines the magnitude of the deviatoric stress
are soil constants. The first equation determines the magnitude of the deviatoric stress 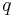 needed to keep the soil flowing continuously as the product of a frictional constant
needed to keep the soil flowing continuously as the product of a frictional constant 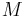 (capital
(capital 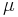 ) and the mean effective stress
) and the mean effective stress 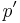 . The second equation states that the specific volume
. The second equation states that the specific volume 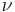 occupied by unit volume of flowing particles will decrease as the logarithm of the mean effective stress increases.
occupied by unit volume of flowing particles will decrease as the logarithm of the mean effective stress increases.
History
In an attempt to advance soil testing techniques, Kenneth Harry Roscoe of Cambridge University, in the late forties and early fifties, developed a simple shear apparatus in which his successive students attempted to study the changes in conditions in the shear zone both in sand and in clay soils. In 1958 a study of the yielding of soil based on some Cambridge data of the simple shear apparatus tests, and on much more extensive data of triaxial tests at Imperial College London from research led by Professor Sir Alec Skempton at the Imperial Geotechnical Laboratories, led to the publication of the critical state concept (Roscoe, Schofield & Wroth 1958).
Roscoe obtained his undergraduate degree in mechanical engineering[1] and his experiences trying to create tunnels to escape when held as a prisoner of war by the Nazis during WWII introduced him to soil mechanics[1]. Subsequent to this 1958 paper, concepts of plasticity were introduced by Schofield and publa classic text book (Schofield & Wroth 1968). Schofield was taught at Cambridge by Prof. John Baker, a structural engineer who was a strong believer in designing structures that would fail "plastically". Prof. Baker's theories strongly influenced Schofield's thinking on soil shear. Prof. Baker's views were developed from his pre-war work on steel structures and further informed by his wartime experiences assessing blast-damaged structures and with the design of the "Morrison Shelter", an air-raid shelter which could be located indoors (Schofield 2006).
Original Cam-Clay Model
The Original Cam-Clay model is based on the assumption that the soil is isotropic, elasto-plastic, deforms as a continuum, and it is not affected by creep. The yield surface of the Cam clay model is described by a log arc.
Modified Cam-Clay Model
Professor John Burland of Imperial College who worked with Professor Roscoe is credited with the development of the modified version of the original model. The difference between the Cam Clay and the Modified Cam Clay [2] (MCC) is that the yield surface of the MCC is described by an ellipse and therefore the plastic strain increment vector (which is vertical to the yield surface) for the largest value of the mean effective stress is horizontal, and hence no incremental deviatoric plastic strain takes place for a change in mean effective stress. This is very convenient for constitutive modelling in numerical analysis, especially finite element analysis, where numerical stability issues are important (as a curve needs to be continuous in order to be differentiable).
Notes
- ^ a b Oxford Dictionary of National Biography, 1961-1970, entry on Roscoe, Kenneth Harry, pp 894-896
- ^ Roscoe K.H. and Burland J.B., 1968, On the generalised stress-strain behaviour of ‘wet’ clay, Eng. plasticity, Cambridge Univ. Press, 535-609
References
- Roscoe, K. H.; Schofield, A. N.; Wroth, C. P. (1958), "On the Yielding of Soils", Geotechnique 8: 22–53
- Schofield, A. N.; Wroth, C. P. (1968), Critical State Soil Mechanics, McGraw-Hill, pp. 310, ISBN 978-0641940484, http://www.geotechnique.info/
- Schofield, A. N. (2006), Disturbed soil properties and geotechnical design, Thomas Telford, pp. 216, ISBN 978-0727729828, http://www.amazon.com/Disturbed-Soil-Properties-Geotechnical-Design/dp/0727729829/ref=sr_1_1?ie=UTF8&s=books&qid=1242332936&sr=8-1